在Starccm+中进行物理运动相关计算时，需要输入相对于质心与指定参考系的转动惯量，记录如下：

转动惯量与惯性张量

惯性张量是一个二阶张量，即是一个3阶矩阵。

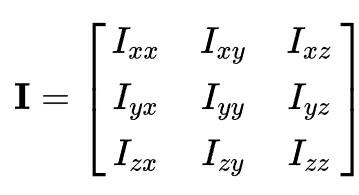
这个惯性张量的计算矩阵可以计算空间中任意一点。其中惯性张量中矩阵对角元素即$I_{xx}$、$I_{yy}$、$I_{zz}$就是绕着x、y和z轴的转动惯量。而$I_{ij}\left(i\ne j\right)$则称之为惯性积。

转动惯量的计算

转动惯量的定义

指的是刚体绕轴旋转时惯性的度量，用字母I或者J来表示，在经典力学里，转动惯量又称之为质量惯性矩，简称惯矩，单位是kg.m2.
转动惯量的描述是刚体质量对于转轴的集中度，质量越集中，转动惯量越小。

转动惯量的计算

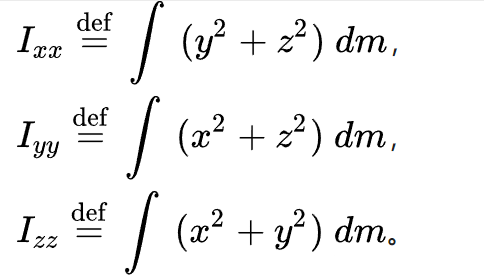
也就是$I=m·r^2$理解上就是某质点绕着某条轴渲染而产生的转动惯量。其中转动半径 r 就是该质点到该轴的距离，从表达式上来看，根据勾股定理，可以分解成投影到另外两个面上的距离的平方和。

惯性积的计算

惯性积的定义

质量元素与至各平面的垂直距离的乘积。
惯性积反应了刚体的质量分布相对于坐标轴（坐标平面）的对称度，对称性越好，惯性积越趋于0.

惯性积的计算

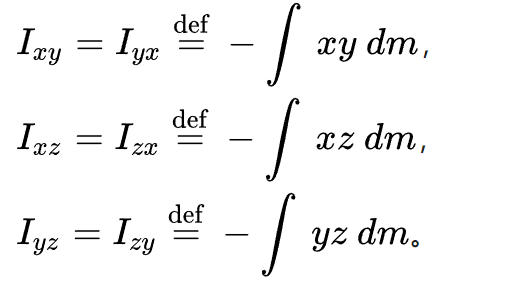
总结

上面的文字对转动惯量与惯性积的定义、物理含义及计算方法做了说明。然后，在实际计算过程中，针对特定的物理模型，可以使用SW的统计功能，直接计算得到。

参考资料链接：

[空间刚体转动惯量 - JadeCicada - 博客园 (cnblogs.com)](https://www.cnblogs.com/butterflybay/p/13245828.html)
[刚体转动的惯性张量和转动惯量的区别和联系_beidou111的博客-CSDN博客](https://blog.csdn.net/weixin_43940314/article/details/123995079)