序: 题目概览
![[附件/Pasted image 20250802203312.png||700]]
0、理论基础
0.1 二叉树的高度和深度
(对某个节点来说)
深度是指从根节点到该节点的最长简单路径边的条数;
高度是指从最下面的叶子节点到该节点的最长简单路径边的条数;
(对二叉树)
深度是从根节点数到它的叶节点;
高度是从叶节点数到它的根节点;
注意: 树的深度和高度一样,但是具体到树的某个节点,其深度和高度不一样。
![[附件/Pasted image 20250802212942.png]]
如图:树的高度和深度都为4(看层数);
节点8的深度为3;节点9的高度为2;
0.2 二叉树的种类
0.2.1 满二叉树
如果一颗二叉树只有度为0的节点和度为2的节点,并且度为0的节点在同一层中,则这颗二叉树成为满二叉树。
![[附件/Pasted image 20250802214351.png||400]]
也可以成为深度为k,则总节点数为2^k - 1
0.2.2 完全二叉树
除了最底层节点没有填完,其余每层节点都达到最大值,并且最下面一层的节点都集中在该层最左侧位置。
若最底层为第h层,则该层包含1~2^(h-1)个节点。
![[附件/Pasted image 20250802214628.png||600]]
0.2.3 二叉搜索数
二叉搜索树有数值,二叉搜索树是一个有序数。
左子树节点值都小于根节点值。
右子树节点值都大于根节点值。
![[附件/Pasted image 20250802214921.png||600]]
0.2.4 平衡二叉搜索树
平衡二叉搜索数,又被称为AVL(Adelson-Velsky and Landis),要么是一颗空树,要么左右两子树高度绝对值不超过1。
![[附件/Pasted image 20250802215215.png||600]]
C++中map、set、multimap,multiset的底层实现都是平衡二叉搜索树,所以map、set的增删操作时间时间复杂度是logn。
0.3 二叉树的存储方式
分为链式存储和顺序存储两种方式,前者使用指针实现,后者使用数组实现。
链式存储,示意图如下:
![[附件/Pasted image 20250802215705.png||700]]
顺序存储(使用数组),如下图所示。
![[附件/Pasted image 20250802215814.png||700]]
如果父节点的数组下标是 i,那么它的左孩子就是 i 2 + 1,右孩子就是 i 2 + 2。
但是用链式表示的二叉树,更有利于我们理解,所以一般我们都是用链式存储二叉树。
0.4 二叉树的遍历方式
主要有深度优先遍历和广度优先遍历。
深度优先遍历:先往深走,遇到叶子节点再往回走。(递归法实现、迭代法实现)
广度优先遍历:一层一层遍历。(迭代法实现)
深度优先遍历的拓展:(要点:前中后指的是中间节点的位置即可。)
- 前序遍历:中左右
- 中序遍历:中左右
- 后续遍历:左右中
例如:
![[附件/Pasted image 20250802220426.png||700]]
0.5 二叉树的定义
C++ 代码如下
struct TreeNode {
int val;
TreeNode *left;
TreeNode *right;
TreeNode(int x) : val(x), left(NULL), right(NULL) {}
};
1 二叉树的递归遍历(力扣:144、145、94)
1.1 递归原理及具体实现
- 确定递归函数的参数和返回值;确定哪些参数是需要处理的,然后就在递归函数里加上这个参数,并且还要明确每次递归的返回值及返回类型。
- 确定终止条件:终止条件务必要清楚。
确定单层递归逻辑:即每一层递归要处理的数据,也就是会重复调用自己来实现递归的过程。
以前序遍历举例:class Solution { public: void traversal(TreeNode* cur, vector<int>& vec) { if (cur == NULL) return; vec.push_back(cur->val); // 中 traversal(cur->left, vec); // 左 traversal(cur->right, vec); // 右 } vector<int> preorderTraversal(TreeNode* root) { vector<int> result; traversal(root, result); return result; } };
1.2 力扣144:前序遍历
1.2.1 题目描述
给你二叉树的根节点 root ,返回它节点值的 前序 遍历。
示例 1:
输入:root = [1,null,2,3]
输出:[1,2,3]
解释:
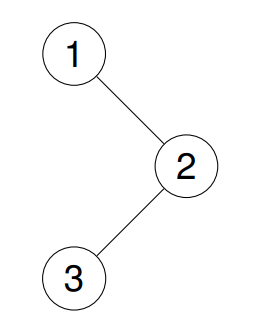
示例 2:
输入:root = [1,2,3,4,5,null,8,null,null,6,7,9]
输出:[1,2,4,5,6,7,3,8,9]
解释:
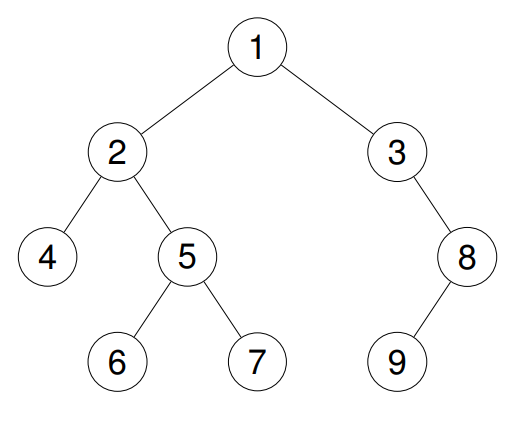
示例 3:
输入:root = []
输出:[]
示例 4:
输入:root = [1]
输出:[1]
1.2.2 题目解析
(解析 = nullptr)
1.2.3 具体代码
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
//遍历的实现
void traversal(TreeNode* cur, vector<int>& result){
if(cur == nullptr) return; //终止条件
result.push_back(cur->val); //具体实现
traversal(cur->left, result);
traversal(cur->right, result);
}
vector<int> preorderTraversal(TreeNode* root) {
vector<int> result; //定义结果数组
traversal(root, result);
return result;
}
};1.3 力扣145:后续遍历
1.3.1 题目描述
给你一棵二叉树的根节点 root ,返回其节点值的 后序遍历 。
示例 1:
输入:root = [1,null,2,3]
输出:[3,2,1]
解释:

1.3.2 题目解析
(解析 = nullptr)
1.3.3 具体代码
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
void traversal(TreeNode* cur, vector<int> &result){
if(cur == nullptr) return;
traversal(cur->left, result);
traversal(cur->right, result);
result.push_back(cur->val);
}
vector<int> postorderTraversal(TreeNode* root) {
vector<int> result;
traversal(root, result);
return result;
}
};1.4 力扣94:中序遍历
1.4.1 题目描述
给定数组,中序遍历
1.4.2 题目解析
nullptr
1.4.3 具体代码
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
void traversal(TreeNode* cur, vector<int> &result){
if(cur == nullptr) return;
traversal(cur->left, result);
result.push_back(cur->val);
traversal(cur->right, result);
}
vector<int> inorderTraversal(TreeNode* root) {
vector<int> result;
traversal(root, result);
return result;
}
};2 二叉树的层序遍历
对应力扣102、107、199、637、429、515、116、117、104、111这10道题目。
2.1 代码模板
class Solution {
public:
vector<vector<int>> levelOrder(TreeNode* root) {
queue<TreeNode*> que; //构建一个储存TreeNode指针的队列
if (root != NULL) que.push(root); //如果根节点不为空,则将其加入队列
vector<vector<int>> result; //构建用于存储最终结果的二维数组
//遍历队列核心代码
//主要队列不为空,就继续处理
while (!que.empty()) {
int size = que.size(); //记录当前层的大小,便于后续处理,这里的数据是后面执行过程中添加进去的。
vector<int> vec; //用于储存当前层的节点值
//遍历当前层的所有节点
for (int i = 0; i < size; i++) {
TreeNode* node = que.front(); //获取队首节点
que.pop(); //弹出队首节点
vec.push_back(node->val); //将当前节点的值加入当前层的数组
if (node->left) que.push(node->left); //将当前节点的子节点加入队列(为下一层做遍历)
if (node->right) que.push(node->right);
}
result.push_back(vec); //将当前层的结果加入最终结果
}
return result; //返回层序遍历的结果
}
};
评论区(暂无评论)